Check Y-o-Y Triangle Inflation Rates

Check for Year-on-Year Inflation rates down the columns of a run-off triangle

Usage

checkTriangleInflation(Triangle)

Arguments

Triangle: average claim amounts triangle. Assume columns are the development period, use transpose otherwise. A (mxn)-matrix $C_{ik}$ which is filled for $k \leq n+1-i; i=1,\ldots,m; m\geq n $, see qpaid for how to use (mxn)-development triangles with m<n, say higher development period frequency (e.g quarterly) than origin period frequency (e.g accident years).

Details

The sensitivity of projections of ultimate losses based on incurred loss development factors to changes in the adequacy level of case reserves increases significantly for the long-tail lines. In particular, if the adequacy of the case reserve is changing, the estimates of ultimate losses based on reported claims could be severely distorted.

The function fits an exponential inflation model that takes the form of: $$Y=a*(1+b)^x$$ where $Y$ represents the inflated claim amount, $a$ represents the claim amount at the beginning of each period (e.g. AY=0), $b$ is the inflation rate and $x$ is the time (e.g. AY).

Fitting such a model on the average level of the case outstanding (or any other average claim amount) for each development period, it is possible to appreciate the inflation rate that has affected the average case reserve.

It is necessary to check the inflation on average amounts, otherwise the estimates may be distorted due to an increase in the number of claims rather than an actual increase in the inflation level.

If the level of inflation is material, it would be necessary to adjust each cell in the triangle.
This is to to have each diagonal in the triangle at the same level as the latest diagonal (i.e. latest valuation). This adjustment would prevent distortions in the estimates caused by inflation and not by actual variations in the claim experience.

Value

checkTriangleInflation returns a list with the following elements

Triangle: Input triangle
summ_table: summary table showing the inflation rate, the $R^2$ of the regression and the number of points used

References

Berquist, J.R. and Sherman, R.E., Loss Reserve Adequacy Testing: A Comprehensive, Systematic Approach, Proceedings of the Casualty Actuarial Society, LXIV, 1977, pp.123-184.

Author

Marco De Virgilis devirgilis.marco@gmail.com

Examples

# Create a triangle of average outstanding claims as the ratio between O/S Claims 
# and Open Claims (i.e. the number of outstanding claims)
avg <- MedMal$MedMalOutstanding / MedMal$MedMalOpen

# Check the level of average inflation Y-o-Y
test<-checkTriangleInflation(avg)

# Plot the results
# A model of exponential inflation fits quite well the level of average O/S claims
# This is particularly evident for DP 1,2,3
plot(test)


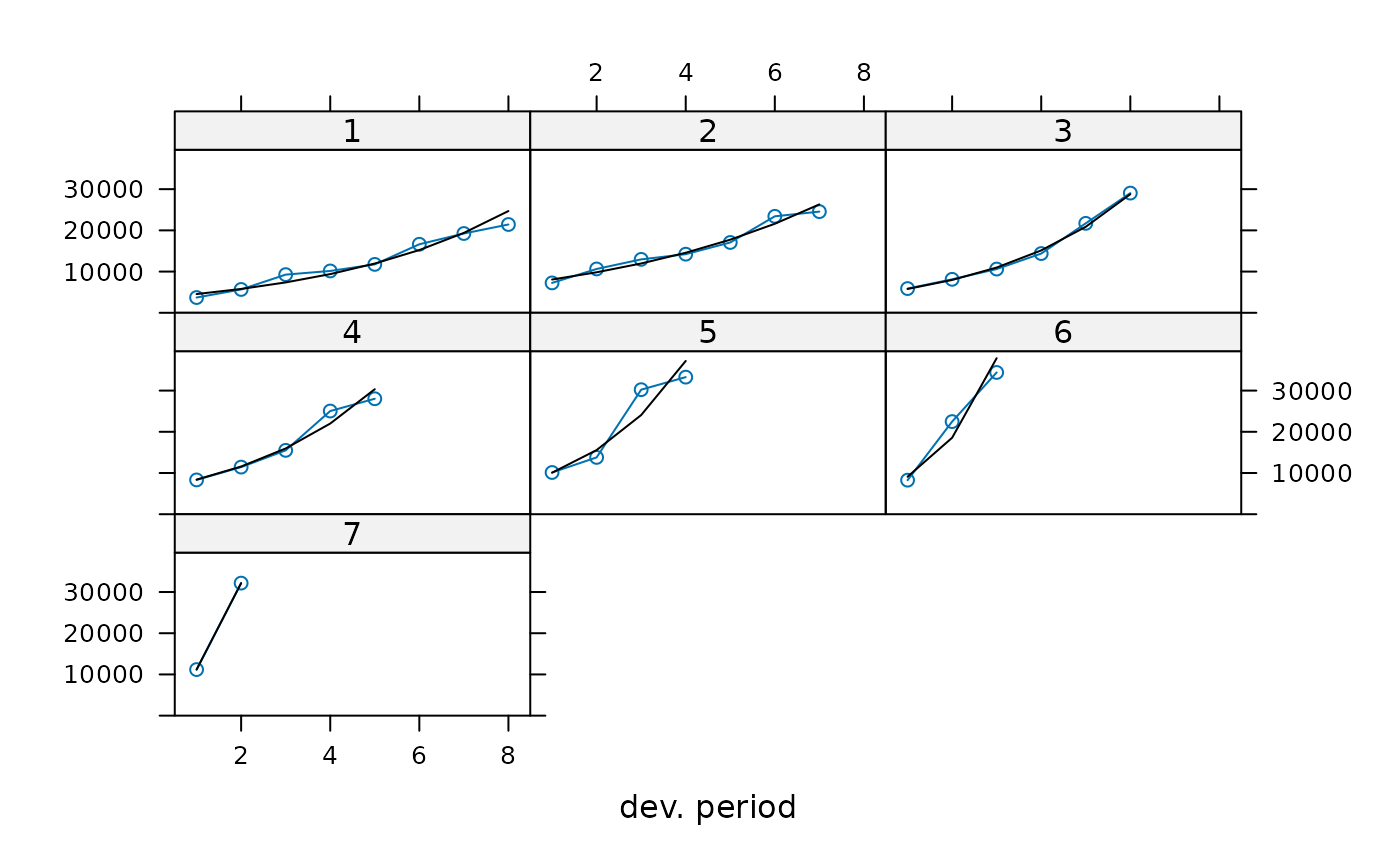# Get the summary in an analytical way to observe the ratios and the number of points used
summary(test)
#>                1         2         3         4         5         6        7
#> rate   0.1561905 0.2949749 0.3110902 0.3417400 0.3296170 0.3216367 0.276155
#> R2     0.7995755 0.8946321 0.8578738 0.9405004 0.9887844 0.9831351 1.000000
#> Points 8.0000000 7.0000000 6.0000000 5.0000000 4.0000000 3.0000000 2.000000

# Print the output
print(test) 
#> Triangle Inflation Calculation
#> 
#>                1         2         3         4         5         6        7
#> rate   0.1561905 0.2949749 0.3110902 0.3417400 0.3296170 0.3216367 0.276155
#> R2     0.7995755 0.8946321 0.8578738 0.9405004 0.9887844 0.9831351 1.000000
#> Points 8.0000000 7.0000000 6.0000000 5.0000000 4.0000000 3.0000000 2.000000
# There is an inflation level equal to .15 at the first development period. It would be 
# appropriate to adjust the triangle before proceeding with any estimate method.